Armchair Graphene Nanoribbon Bandgap Width 3p 3p+1 3p+2
umccalltoaction
Nov 17, 2025 · 10 min read
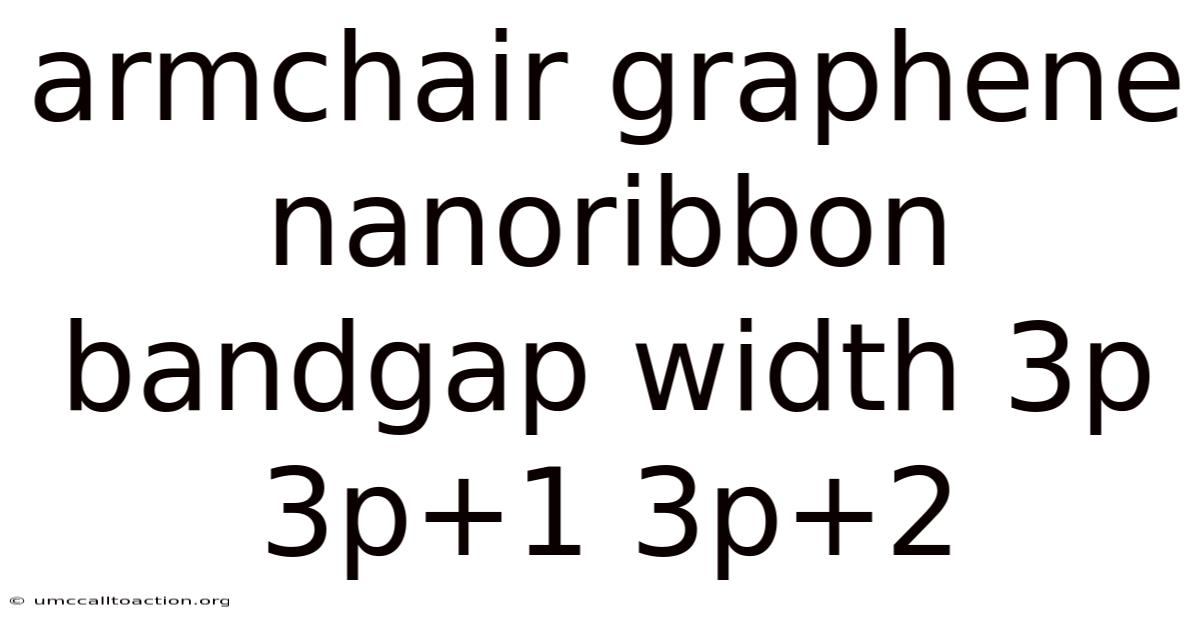
Table of Contents
Graphene nanoribbons (GNRs), strips of graphene with widths on the nanometer scale, possess electronic properties highly sensitive to their structural characteristics, particularly their width and edge structure. This sensitivity opens avenues for tailoring GNRs for specific applications in nanoelectronics, spintronics, and optoelectronics. A crucial parameter dictating these applications is the bandgap, which dictates the energy required for electrons to jump from the valence band to the conduction band, effectively determining the material's conductivity. Armchair graphene nanoribbons (AGNRs), characterized by their armchair-shaped edges, exhibit a unique bandgap behavior related to their width, often described using the "3p, 3p+1, 3p+2" family classification. Understanding this classification and its impact on the bandgap is fundamental for designing AGNR-based devices with desired electronic properties.
Armchair Graphene Nanoribbons: A Primer
AGNRs are defined by their width, represented by the number of carbon atoms across the ribbon. These widths are commonly classified into three families based on their remainder when divided by three: 3p, 3p+1, and 3p+2, where 'p' is an integer. This seemingly simple classification has profound implications for the electronic band structure of the AGNR.
- 3p AGNRs: These ribbons have a width that is a multiple of three.
- 3p+1 AGNRs: The width of these ribbons leaves a remainder of one when divided by three.
- 3p+2 AGNRs: These ribbons have a width that leaves a remainder of two when divided by three.
The different electronic behaviors of these three families stem from the quantum confinement effects within the narrow GNR and the subtle variations in edge states arising from the armchair configuration. These edge states significantly influence the overall electronic structure and, consequently, the bandgap.
The Bandgap and Quantum Confinement
The bandgap in a material is the energy difference between the valence band (the highest energy level occupied by electrons at absolute zero) and the conduction band (the lowest energy level where electrons can move freely). In bulk graphene, the valence and conduction bands meet at the Dirac point, making it a zero-bandgap semiconductor or a semimetal. However, when graphene is confined into a nanoribbon, quantum confinement effects come into play.
Quantum confinement arises because electrons are restricted to move within a smaller space. This restriction leads to the quantization of electron energy levels, meaning that electrons can only exist at specific energy levels. This is analogous to a particle in a box, where the energy levels are inversely proportional to the size of the box. In AGNRs, the width of the ribbon acts as the "box," and as the width decreases, the energy levels become more spaced out, leading to a larger bandgap.
Bandgap Modulation in 3p, 3p+1, and 3p+2 AGNRs
While quantum confinement generally predicts an inverse relationship between width and bandgap, the 3p, 3p+1, and 3p+2 classification introduces significant nuances. Each family exhibits a distinct dependence of the bandgap on width, largely attributed to the subtle differences in their edge electronic structure.
3p AGNRs: The Smallest Bandgap
AGNRs belonging to the 3p family typically exhibit the smallest bandgaps compared to the other two families for a given width. This is attributed to specific edge states that arise from the particular arrangement of carbon atoms at the armchair edge. These edge states contribute to the formation of energy levels close to the Fermi level (the energy level with a 50% probability of being occupied by an electron at a given temperature), thus reducing the bandgap.
Importantly, even within the 3p family, the relationship between width and bandgap is not perfectly smooth. Computational studies often reveal oscillations in the bandgap as the width increases, reflecting complex interactions between quantum confinement and edge state contributions.
3p+1 AGNRs: An Intermediate Behavior
The 3p+1 family of AGNRs generally shows intermediate bandgap values compared to the 3p and 3p+2 families. Their electronic structure is influenced by a different pattern of edge states, which do not contribute as significantly to reducing the bandgap as in the 3p family. While quantum confinement still plays a crucial role, the specific edge configuration results in a bandgap that is larger than that of the 3p family but typically smaller than that of the 3p+2 family for a similar width.
3p+2 AGNRs: The Largest Bandgap
AGNRs belonging to the 3p+2 family tend to have the largest bandgaps among the three families. This is again linked to the specific electronic structure arising from the armchair edge configuration. The edge states in this family are less prone to create energy levels near the Fermi level, leading to a wider energy separation between the valence and conduction bands. As a result, 3p+2 AGNRs are often considered as promising candidates for applications requiring larger bandgaps.
Beyond Simple Classification: Factors Affecting the Bandgap
While the 3p, 3p+1, and 3p+2 classification provides a useful framework for understanding the bandgap behavior of AGNRs, it is essential to recognize that other factors can significantly influence the electronic properties.
- Edge Termination: The chemical termination of the edges plays a crucial role. Hydrogen passivation is commonly assumed in theoretical calculations, but other terminations like oxygen or hydroxyl groups can drastically alter the edge states and, consequently, the bandgap.
- Edge Reconstruction: The edges of AGNRs are not always perfectly smooth. Edge reconstruction, where the carbon atoms rearrange themselves to minimize energy, can significantly modify the electronic structure and bandgap.
- Defects: Defects within the graphene lattice, such as vacancies or topological defects, can introduce localized states within the bandgap, affecting the overall electronic transport properties.
- External Electric Fields: Applying an external electric field can shift the energy levels and modulate the bandgap of AGNRs. This opens possibilities for creating field-effect transistors based on AGNRs.
- Strain: Applying mechanical strain to an AGNR can also modify its bandgap. Tensile strain generally reduces the bandgap, while compressive strain can increase it.
- Temperature: Temperature affects the electron-phonon interactions and can influence the bandgap, although the effect is usually smaller compared to other factors.
- Substrate Interactions: When an AGNR is placed on a substrate, the interaction between the AGNR and the substrate can alter its electronic properties, including the bandgap.
Computational Methods for Bandgap Determination
Determining the bandgap of AGNRs accurately requires sophisticated computational methods. Several approaches are commonly employed:
- Density Functional Theory (DFT): DFT is a widely used method for calculating the electronic structure of materials. It approximates the many-body Schrödinger equation by using an effective potential that depends on the electron density. DFT calculations can provide reasonably accurate predictions of the bandgap, but they often underestimate the bandgap compared to experimental values due to the inherent limitations of the exchange-correlation functionals used in DFT.
- GW Approximation: The GW approximation is a more advanced method that goes beyond DFT by explicitly considering the electron self-energy. It provides a more accurate description of electron-electron interactions and typically yields more accurate bandgaps than DFT. However, GW calculations are computationally more demanding than DFT calculations.
- Tight-Binding Methods: Tight-binding methods are simpler and computationally less expensive than DFT and GW. They are based on approximating the electronic structure by considering only the interactions between nearest-neighbor atoms. Tight-binding methods can provide a qualitative understanding of the bandgap behavior of AGNRs, but they are less accurate than DFT and GW.
- Empirical Models: Empirical models are based on fitting experimental data or higher-level calculations to a simple analytical expression. These models can be useful for quickly estimating the bandgap of AGNRs, but they are limited by the accuracy of the data they are based on.
Applications of AGNRs Based on Bandgap Engineering
The ability to tune the bandgap of AGNRs by controlling their width and edge structure opens a wide range of potential applications:
- Transistors: AGNRs can be used as the channel material in field-effect transistors (FETs). By controlling the bandgap, the on/off ratio and operating voltage of the transistor can be tailored. The 3p+2 family, with its larger bandgap, is particularly attractive for high-performance transistors.
- Photodetectors: AGNRs can be used as photodetectors, where they absorb light and generate an electrical signal. The bandgap determines the wavelength of light that can be detected. By tuning the bandgap, AGNR photodetectors can be designed to operate in specific spectral regions.
- Sensors: AGNRs are highly sensitive to their environment, and their electronic properties can be affected by the presence of certain molecules. This makes them suitable for use as sensors for detecting gases, chemicals, or biomolecules. Changes in the bandgap can be used to detect the presence of these substances.
- Solar Cells: AGNRs can be used as the active material in solar cells. The bandgap determines the efficiency with which the solar cell can convert sunlight into electricity.
- Thermoelectric Devices: AGNRs can be used in thermoelectric devices, which convert heat energy into electrical energy and vice versa. The bandgap plays a role in determining the thermoelectric efficiency of the material.
- Spintronics: By introducing magnetic dopants or creating edge magnetization, AGNRs can be used in spintronic devices, which utilize the spin of electrons in addition to their charge for information processing and storage.
Challenges and Future Directions
While AGNRs hold tremendous promise, several challenges need to be addressed before their widespread adoption in technological applications:
- Precise Synthesis: Synthesizing AGNRs with precise control over their width and edge structure remains a significant challenge. Current fabrication methods often result in AGNRs with varying widths and defects. Bottom-up synthesis approaches, where AGNRs are assembled from molecular precursors, offer a promising route to achieving better control.
- Edge Control: Controlling the edge termination and preventing edge reconstruction are crucial for achieving the desired electronic properties. Developing methods for passivating the edges with specific chemical groups is an active area of research.
- Characterization: Accurately characterizing the width, edge structure, and electronic properties of AGNRs is essential for understanding their behavior and optimizing their performance. Developing advanced characterization techniques with high spatial resolution is an ongoing effort.
- Integration: Integrating AGNRs into electronic devices in a reliable and scalable manner is another challenge. Developing methods for aligning and contacting AGNRs is crucial for creating functional devices.
- Stability: Ensuring the long-term stability of AGNRs under various operating conditions is important for practical applications. Protecting AGNRs from oxidation and degradation is an area of concern.
Future research directions in AGNRs include:
- Developing new synthesis methods for AGNRs with precise control over their width, edge structure, and doping.
- Exploring novel edge terminations and passivation strategies to tune the electronic properties of AGNRs.
- Investigating the effects of defects, strain, and electric fields on the bandgap and transport properties of AGNRs.
- Developing new device architectures based on AGNRs for transistors, photodetectors, sensors, and other applications.
- Exploring the potential of AGNRs for spintronics and quantum computing.
Conclusion
The bandgap of armchair graphene nanoribbons is intricately linked to their width, particularly as categorized by the 3p, 3p+1, and 3p+2 families. This classification provides a valuable framework for understanding and manipulating the electronic properties of these materials. However, factors such as edge termination, defects, and external influences also play significant roles. Through continued research and development, AGNRs hold the potential to revolutionize nanoelectronics and pave the way for innovative technological applications. By overcoming the existing challenges and exploring new avenues of research, the promise of AGNRs as versatile building blocks for future electronic devices can be fully realized. Their tunable electronic properties, combined with their potential for integration into various devices, make them a fascinating and promising area of study in materials science and nanotechnology.
Latest Posts
Latest Posts
-
Do Iron Tablets Make You Gain Weight
Nov 18, 2025
-
Do Rabies Virus Survive In Water
Nov 18, 2025
-
Tarlatamab In Small Cell Lung Cancer After Platinum Based Chemotherapy
Nov 18, 2025
-
What Can Dna Fingerprinting Be Used For
Nov 18, 2025
-
Which Of The Following Is True Of All Eukaryotic Cells
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about Armchair Graphene Nanoribbon Bandgap Width 3p 3p+1 3p+2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.