120 X 0.3 90 X 0.7
umccalltoaction
Nov 16, 2025 · 8 min read
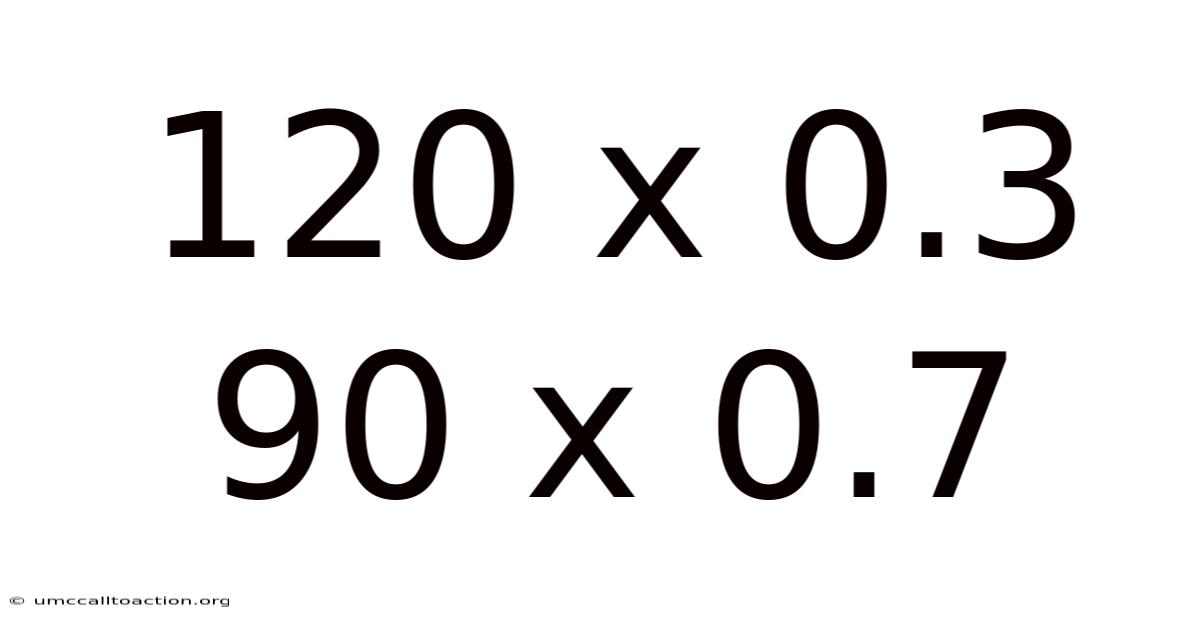
Table of Contents
Unpacking the Math: 120 x 0.3 and 90 x 0.7 - A Comprehensive Guide
Understanding multiplication involving decimals is a fundamental skill in mathematics with widespread applications in everyday life. Whether calculating discounts, figuring out proportions, or even understanding statistics, grasping the mechanics of multiplying numbers with decimal points is crucial. This article provides a comprehensive breakdown of the calculations 120 x 0.3 and 90 x 0.7, exploring the underlying principles, practical applications, and potential pitfalls to avoid. We'll delve into various methods for solving these problems, offering insights that can be applied to a wide range of similar calculations.
Understanding Decimal Multiplication: The Foundation
Before diving into the specific calculations, let's lay a solid foundation in the principles of decimal multiplication. A decimal number is a number that includes a decimal point, representing a fraction or part of a whole. When multiplying with decimals, we are essentially finding a fraction of a number.
- Basic Principle: When multiplying a whole number by a decimal less than 1 (like 0.3 or 0.7), the result will always be less than the original whole number. This is because we are taking a fraction of that number.
- The Decimal Point's Role: The position of the decimal point in the final answer is crucial. It's determined by the total number of decimal places in the numbers being multiplied.
- Place Value Matters: Understanding place value (ones, tens, tenths, hundredths, etc.) is essential for correctly aligning numbers during multiplication and placing the decimal point in the final answer.
Calculating 120 x 0.3: Step-by-Step
Let's break down the calculation of 120 x 0.3 into manageable steps.
Method 1: Traditional Multiplication
- Ignore the Decimal: Initially, treat 0.3 as the whole number 3. Multiply 120 by 3: 120 x 3 = 360
- Count Decimal Places: In the original problem (120 x 0.3), the number 0.3 has one decimal place.
- Place the Decimal Point: Starting from the rightmost digit of the result (360), move the decimal point one place to the left. This gives us 36.0.
- Simplify: 36.0 is the same as 36.
Therefore, 120 x 0.3 = 36
Method 2: Fraction Conversion
- Convert Decimal to Fraction: Convert 0.3 to its fractional equivalent. 0.3 is equal to 3/10.
- Multiply by the Fraction: Multiply 120 by 3/10: 120 x (3/10) = (120 x 3) / 10 = 360 / 10
- Simplify: Divide 360 by 10, which gives us 36.
Again, 120 x 0.3 = 36
Method 3: Mental Math (Decomposition)
- Think of 0.3 as 3 x 0.1: Rewrite the problem as 120 x (3 x 0.1)
- Multiply by 3: 120 x 3 = 360
- Multiply by 0.1 (or Divide by 10): Multiplying by 0.1 is the same as dividing by 10. 360 / 10 = 36.
This method relies on understanding that multiplying by 0.1 is equivalent to finding 1/10th of the number.
Calculating 90 x 0.7: A Similar Approach
Now, let's apply the same methods to calculate 90 x 0.7.
Method 1: Traditional Multiplication
- Ignore the Decimal: Multiply 90 by 7: 90 x 7 = 630
- Count Decimal Places: In the original problem (90 x 0.7), the number 0.7 has one decimal place.
- Place the Decimal Point: Move the decimal point one place to the left in the result (630), resulting in 63.0.
- Simplify: 63.0 is the same as 63.
Therefore, 90 x 0.7 = 63
Method 2: Fraction Conversion
- Convert Decimal to Fraction: Convert 0.7 to its fractional equivalent. 0.7 is equal to 7/10.
- Multiply by the Fraction: Multiply 90 by 7/10: 90 x (7/10) = (90 x 7) / 10 = 630 / 10
- Simplify: Divide 630 by 10, which gives us 63.
Again, 90 x 0.7 = 63
Method 3: Mental Math (Decomposition)
- Think of 0.7 as 7 x 0.1: Rewrite the problem as 90 x (7 x 0.1)
- Multiply by 7: 90 x 7 = 630
- Multiply by 0.1 (or Divide by 10): 630 / 10 = 63.
This method reinforces the principle of using place value for efficient mental calculations.
Practical Applications in Real Life
Understanding how to multiply with decimals is essential for various real-world scenarios. Here are a few examples:
- Discounts and Sales: Calculating discounts is a prime example. If an item priced at $120 is on sale for 30% off (0.3), the discount amount is 120 x 0.3 = $36. The final price would be $120 - $36 = $84. Similarly, if an item costs $90 and you have a 70% (0.7) off coupon, the discount is $90 x 0.7 = $63, and the final price is $90 - $63 = $27.
- Calculating Tips: When dining out, calculating the tip often involves multiplying the bill amount by a decimal representing the tip percentage. For example, a $90 bill with a 20% tip (0.2) would require you to calculate $90 x 0.2 = $18 tip.
- Percentage Increases: Businesses use this skill to calculate price increases. If a product that costs $120 has a price increase of 30% (0.3), the increase amount is 120 x 0.3 = $36.
- Currency Exchange: When traveling, you often need to convert currency using exchange rates, which are often expressed as decimals. Multiplying the amount you want to convert by the exchange rate helps you determine the equivalent amount in the new currency.
- Cooking and Baking: Adjusting recipe quantities frequently involves multiplying ingredient amounts by decimals to scale the recipe up or down.
Common Mistakes to Avoid
While the process of multiplying with decimals is straightforward, certain common errors can lead to incorrect answers. Being aware of these pitfalls can help you avoid them.
- Incorrect Decimal Placement: The most common mistake is misplacing the decimal point in the final answer. Always remember to count the total number of decimal places in the numbers being multiplied and apply that count to the result.
- Forgetting to Account for Zeroes: When multiplying numbers with trailing zeroes, be careful not to overlook their impact on the final answer. Ensure you correctly account for the zeroes when placing the decimal point.
- Rounding Errors: If you are dealing with decimals that need to be rounded, do the rounding after the multiplication is complete. Rounding before multiplying can lead to significant errors in the final result.
- Misunderstanding Place Value: A weak understanding of place value can lead to alignment errors during multiplication. Always ensure that numbers are correctly aligned based on their place value (ones, tens, tenths, etc.).
- Calculator Dependence: While calculators can be helpful, relying on them exclusively can hinder your understanding of the underlying principles. Practice performing decimal multiplication manually to develop a solid understanding of the concepts.
Advanced Techniques and Considerations
Beyond the basic methods, there are some advanced techniques and considerations that can further enhance your ability to work with decimal multiplication.
- Scientific Notation: When dealing with very large or very small numbers, scientific notation can simplify multiplication. Convert the numbers to scientific notation, multiply the coefficients, and add the exponents.
- Estimation: Before performing the actual multiplication, estimate the answer. This helps you quickly identify if your final answer is reasonable. For example, for 120 x 0.3, you could estimate that 0.3 is close to 1/3, and 1/3 of 120 is 40. Your actual answer should be close to 40.
- Using Properties of Multiplication: Leverage the associative and commutative properties of multiplication to simplify calculations. For example, 120 x 0.3 can be rearranged as 0.3 x 120, which might be easier to visualize.
- Understanding Significant Figures: In scientific and engineering contexts, understanding significant figures is critical. The number of significant figures in your result should reflect the precision of the input numbers.
Practice Problems
To solidify your understanding, try solving these practice problems:
- 150 x 0.6 = ?
- 75 x 0.8 = ?
- 200 x 0.25 = ?
- 45 x 0.4 = ?
- 110 x 0.9 = ?
Answers:
- 90
- 60
- 50
- 18
- 99
The Importance of Conceptual Understanding
While memorizing procedures can be helpful, a conceptual understanding of decimal multiplication is crucial for long-term retention and application. Understanding why the methods work, rather than just how, allows you to adapt to different situations and solve problems more creatively.
- Connecting to Fractions: Continuously reinforce the connection between decimals and fractions. This helps visualize what you are actually doing when multiplying with decimals.
- Real-World Context: Always frame decimal multiplication problems in real-world contexts. This makes the math more relatable and meaningful.
- Visual Aids: Use visual aids like number lines or area models to illustrate the process of decimal multiplication.
Conclusion
Mastering multiplication with decimals, exemplified by calculations like 120 x 0.3 and 90 x 0.7, is a fundamental skill with broad applications. By understanding the underlying principles, practicing different calculation methods, and avoiding common mistakes, you can confidently tackle a wide range of decimal multiplication problems. Whether calculating discounts, figuring out proportions, or simply solving everyday mathematical challenges, a solid grasp of decimal multiplication will undoubtedly prove invaluable. Remember that continuous practice and a strong conceptual understanding are the keys to success.
Latest Posts
Latest Posts
-
Are Multi Vitamins Bad For Your Liver
Nov 16, 2025
-
Where Does Synthesis Of Lipids Take Place
Nov 16, 2025
-
Natural Selection Of Mutants That Modify Population Structure
Nov 16, 2025
-
Why Do Histones Bind Tightly To Dna
Nov 16, 2025
-
Tight Junctions Desmosomes And Gap Junctions
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about 120 X 0.3 90 X 0.7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.